Steffen W. R. Werner

Assistant Professor at Virginia Tech, Blacksburg, USA

Research Projects

Research Interests

Context-Aware Learning of Low-Dimensional Controllers

Context-aware Learning Flow Chart The general idea of context-aware learning is to directly learn the task of interest rather than some generic descriptions of the occurring dynamics, which usually demands for lots of data and computational resources to learn an accurate representation of the underlying physics. Thereby, it is possible to restrict to the task-relevant dynamics, which are often simpler than the full underlying physics, such that the data requirements for the training only scale with the task. In this project, we consider the task of learning controllers for dynamical systems from given data.

Data-Driven Reduced-Order Modeling of Mechanical Systems

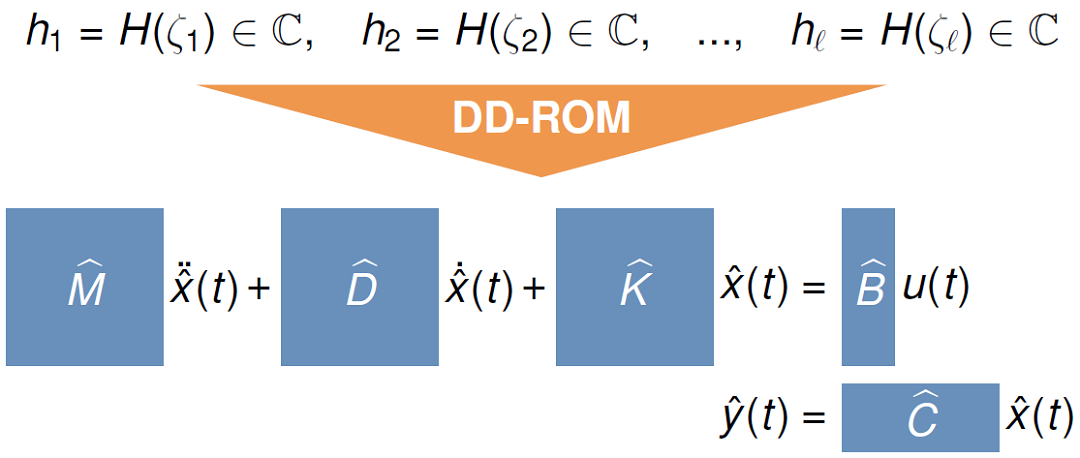Structured Data-Driven Reduced-Order Modeling Data-driven reduced-order modeling is essential in the construction of compact, high-fidelity models from frequency domain data. While there exist already unstructured approaches for data-driven modeling from data, it is of particular interest to retain the physical structure as in the case of structure-preserving model reduction. The main problems arising here are, first of all, to enforce the classical mechanical system structure, which is typically lost in data obtained from the system’s transfer function and second, to receive physically interpretable properties in the resulting matrices such as positive definiteness of mass, damping and stiffness. In this project, we develop extensions of the barycentric form to the case of mechanical systems leading to the extension of known techniques to the learning of structured models from frequency domain data such as the AAA algorithm, the Loewner framework or vector fitting.

Structure-Preserving Model Reduction for Mechanical Systems

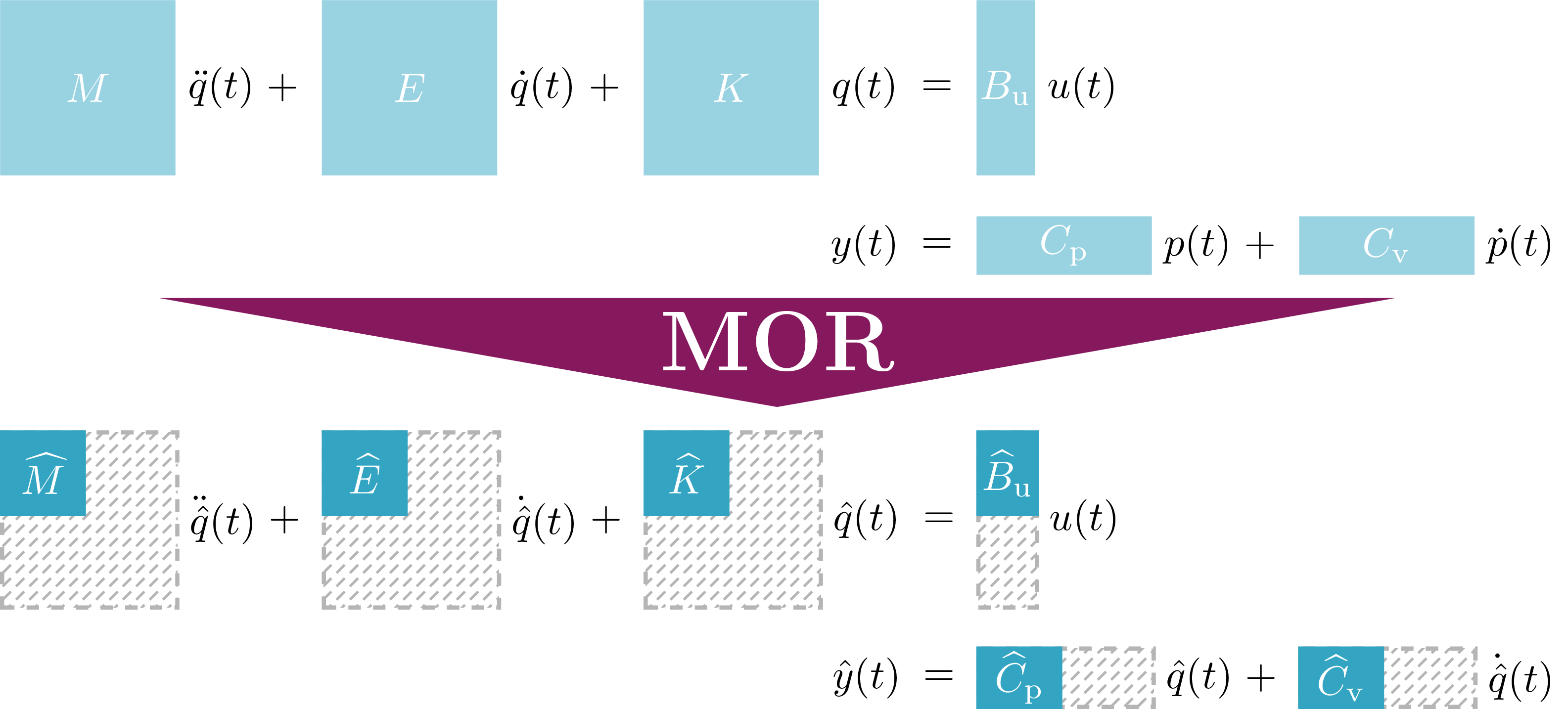Second-Order System MOR For the construction of complex mechanical structures such as bridges, buildings, or vehicles, the use of computer models is nowadays indispensable. Such computer models are typically used to simulate and, if necessary, to optimize the oscillation behavior. For instance, such an optimization is useful to suppress and damp undesired oscillations. Taking into account the input-output structure of the system, modeling of such mechanical structures typically leads to dynamical systems described by second-order ordinary differential equations. Often the system dimension (i. e., the number of masses) is very large. The aim of model reduction is now to approximate the original system by a much smaller one to save a huge amount of computational resources during evaluation of the model. In this project we want to develop new model reduction techniques for second-order mechanical systems that also preserve certain system properties like dissipativity.

Robust Flow Control via HINFBT

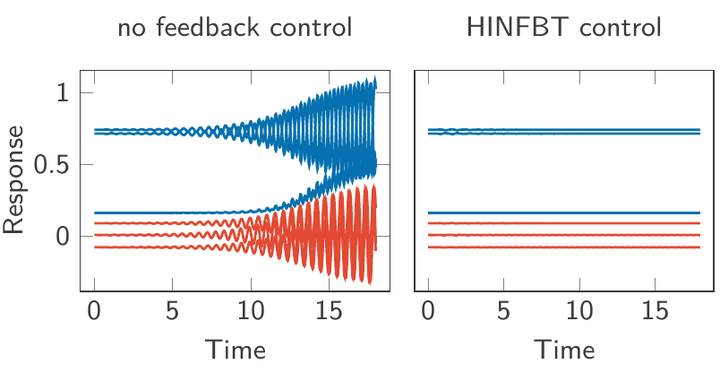Flow Stabilization For the efficient stabilization of flows, controllers of small orders are needed, which also bridge the gap between approximation and model, or model and reality. While there are established construction formulas for robust stabilizing controllers, those usually lead to controllers described by systems of differential equations of the same size as the original system, which makes real time control of the system impossible. In this project, we aim for the construction of such low-order robust stabilizing controllers by employing LQG- and H-Infinity-based model reduction methods and controller theory.

MORLAB – Model Order Reduction LABoratory

MORLAB Logo MORLAB, the Model Order Reduction LABoratory toolbox, is a collection of MATLAB and Octave routines for model order reduction of dense linear time-invariant continuous-time systems. The toolbox contains model reduction methods for standard, descriptor and second-order systems based on the solution of matrix equations. Therefore, also spectral projection based methods for the solution of the corresponding matrix equations are included. See the project website for more information.